Addition Rule

Say there are 2 events A and B. P(A) represents the probability of A occuring and P(B) represents the probability of B occuring.
Here is the question - What is the probability of either A or B occuring? In other words
What is P(AUB)?
\(P(A \cup B)=P(A)+P(B) - P(A \cap B)\)

Example

Say you pick a card from a regular deck of cards, what is the probability that it is either a King or a Heart?
Let A be the event of picking a King and B be the event of picking a Heart.

\(P(A)=\frac{4}{52}\) (As there are 52 cards and 4 kings, one in each suit)

\(P(B)=\frac{13}{52}\) (As there are 52 cards and 13 hearts)

\(P(A \cap B)=\frac{1}{52}\) (As there is 1 card in the whole deck which is a King of Heart)

\(P(A \cup B)=\frac{4}{52}+\frac{13}{52}−\frac{1}{52}=\frac{16}{52}=\frac{4}{13}\)

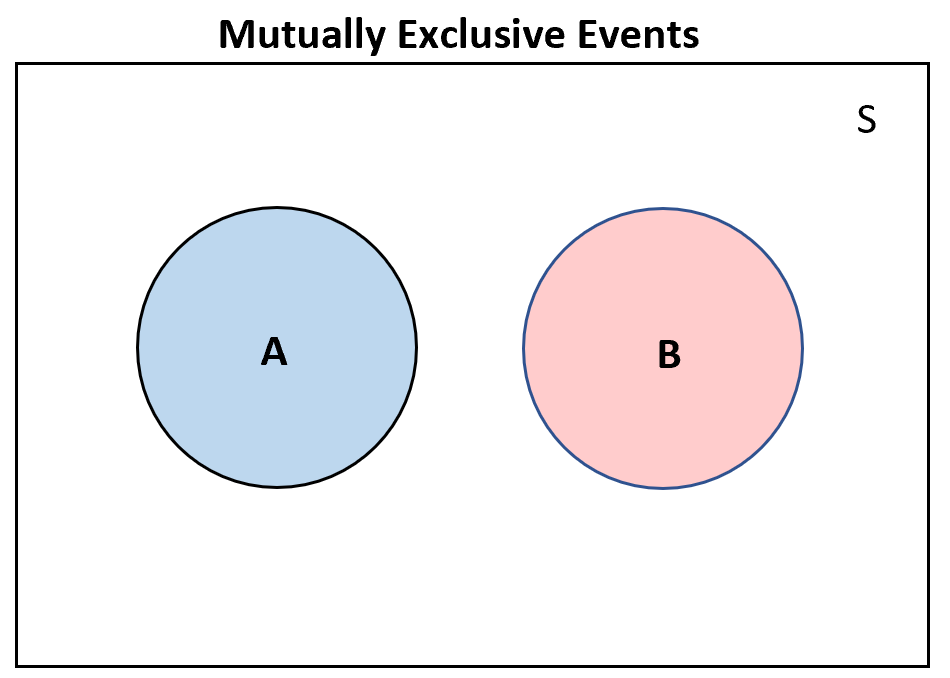
What are mutually exclusive events?

Event A and B are mutually exclusive when \(P(A\cap B)=0\)
For mutually exclusive events \(P(A \cup B)=P(A)+P(B)\)
as \(P(A\cap B) = 0\)