Sets

What are Sets?

A set is a collection of well-defined sets of objects or elements. A set is represented by a capital letter and the elements are placed inside curly brackets. To get a much clear understanding of a set, consider the below example.
A = {1, 2, 3, 4, 5}
In the above example “A” is the set and numbers 1, 2, 3, 4, 5 are the elements or the components of the set. Elements inside a set can be arranged in any order but cannot be duplicated.

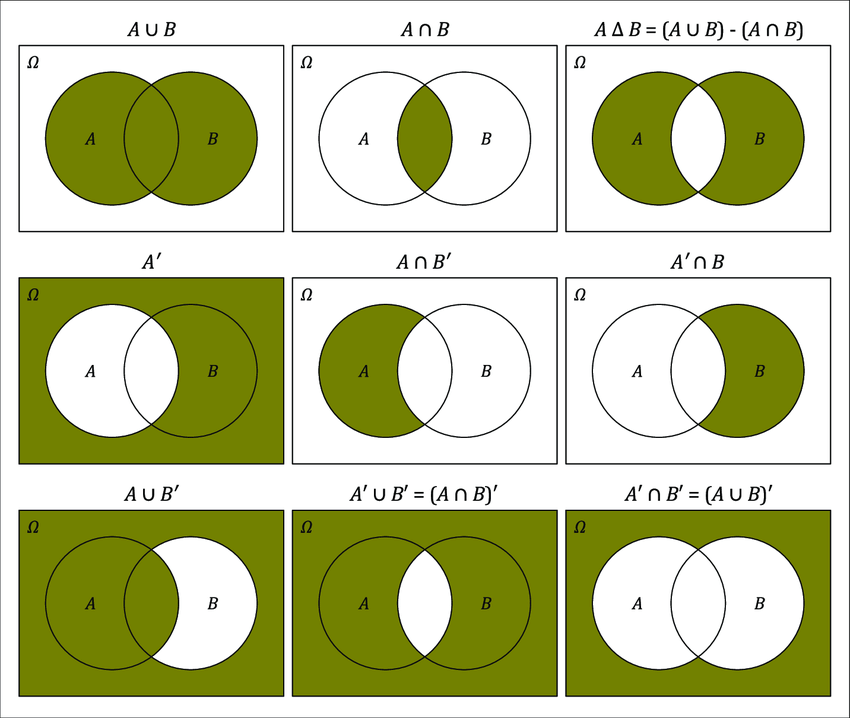
Intersection of sets

The intersection of sets for two given sets will provide another set which consist of all the elements that are common to both sets. The symbol used to denote intersection of sets is “∩”. For example, consider the below two sets A and B.
A = {1, 2, 3, 4, 5}
B = {3,5,7,8}
In the above two sets we can see that the common elements for both the sets are elements 3 and 5. Therefore intersection of the two sets could be denoted as below.
A∩B = {3,5}
Here, the elements in set A intersection B are present in both set A and B

Union of sets

A union of sets is the set that contains all the elements of two given sets. The union of sets is denoted by the symbol “∪”. Consider the below example to further understand the union of two sets.
A = {1, 2, 3, 4, 5}
B = {3,5,7,8}
A∪B = {1, 2, 3, 4, 5, 7, 8}
The elements in A union B set are either present in set A or set B.

Universal Set

A Universal Set is the set of all elements under consideration, denoted by capital U. All other sets are subsets of the universal set.

Compliment of a Set

Say the universal set is U = {1,2,3,4,5,6,7,8}
and A = {3,5,7,8}
Compliment of Set (A’) is a set of all the elements in U and not in A.
So A’ = {1, 2, 4, 6, 7, 8}
Few other operations on sets are illustrated in the diagram above.